唐突ですが$10÷0$の答えは何だと思いますか?
答えは0とか無限と答える人が多いのではないでしょうか。
実際小学校の頃に答えは0と教えられることのある人もいるでしょう。


しかし答えは0でも無限でありません。
そもそも数学では上手く定義できないため0で割るということ自体を避けています。
基本的に数学の世界では0で割るという式は意味のある式ではなく、数学上の哲学の領域になるのです。
ここでは何故0で割ると答えが0や無限大にならない、そして上手く定義できない理由を紹介していきます。
$x÷0(x≠0)$について考える
それでは実際に$x÷0$について見ていきましょう。
まず、ここでは$x$が0ではない場合から説明します。
最もわかりやすいのは引き算をもとに考えていくことです。
具体的に$10÷2=5$という式から考えましょう。
$10÷2=5$…この式は「10から2を何回引いたらそれ以上引けなくなりますか? 答.5回」と言い換えられますね。
この式の割る数2の部分を0に変換してみましょう。
$10÷0=□$…「10から0を何回引いたらそれ以上引けなくなりますか?」こう聞かれると、“何回でも引けるから答えは無限!”と言いたくなりまよね。
ちょっと待ってください。もう少し詳しく見てみましょう。
「10から2を何回引いたらそれ以上引けなくなりますか? 答.5回」この文章はさらに「2を5回足すと10になる」と言い換えられます。
では0で割る式で考えてみましょう。
「0を□回足すと10になる」…何回足しても10にはなりませんね。そうです、答えを出すことが不可能なんです。
以上の文章を式に直してみましょう。
$10÷2=5$
⇒$2×5=10$
というように変換できるので0で割る式も
$10÷0=□$
⇒$0×□=10$
となるはずですよね。0に何を掛けても10にはなりません。
以上のように$x$が0でない場合は$x÷0$は計算すること自体ができないので「不能」となります。
$0÷0$について考える
それでは次に$0÷0$について考えていきましょう。
この式も先ほどの引き算の文章に当てはめてみます。
「0から0を何回引いたらそれ以上引けなくなりますか?」この問題も“何回も引けるから答えは無限大!”とはなりません。
この問題の答えは何回でもいいんです。
0から1回0を引くと0……$0-0=0$
0から2回0を引くと0……$0-0-0=0$
0から3回0を引くと0……$0-0-0-0=0$
このように何回でも答えになってしまうのです。
先ほどと同じように掛け算の式でも確かめてみましょう。
$0÷0=□$
⇒$0×□=0$
とするとやはり□にはどんな数字でも入れることができますね。
以上のこととから$0÷0$は答えを定めることができず「不定」となります。
まとめ
◆$x$が0でないときの$x÷0$の答えは不能
◆$x$が0のとき、つまり$0÷0$の答えは不定
$x÷0=∞$の考え方
ここでは$x÷0=∞$という考え方について紹介していきます。
これまで説明した通り$x÷0=∞$ではないのですがこのような考え方は確かにあります。
ここで重要となるキーワードが無限小です。
無限小は“0に限りなく近くどんな数より小さい数”です。
0.0000000...と永遠に続く数と考えてもらったらよいでしょうか。
とても概念的な数なんです。
ただ無限小数は0に限りなく近いですが0ではありません。
この無限小数と0を区別せず同じものと混同すると∞という答えが説明できます。
小学生の頃に習った反比例のグラフで考えてみましょう。
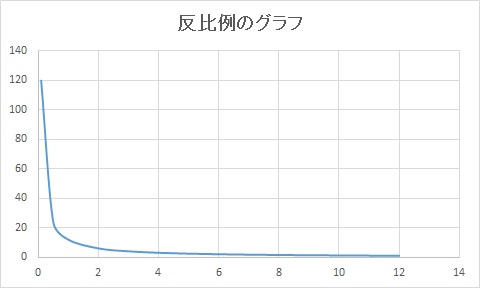
このグラフでxの値を限りなく小さくしていくとyの値は逆に限りなく大きくなっていきますね。
ということは$□÷無限小=無限大$ということになります。
ここで無限小と0を混同すると無限小=0なのだから$□÷0=無限大$とできてしまいます。
簡単に説明しましたが、この考え方はさまざまな矛盾が生じてきます。
よって数学では基本的に、0で割ることはできない、意味がないとしているのです。
まとめ
数学って計算によってすべて答えが導き出せる学問だと思っていませんでしたか?
しかし、“限りなく小さい数”とは?のように哲学的な考え方もあるんです。
そして解明されてない問題や謎もたくさんあるんです。
私は数学に関する専門知識はありませんので、面白い謎や矛盾、そして数学にまつわるストーリーなど紹介していけたらと思います。
